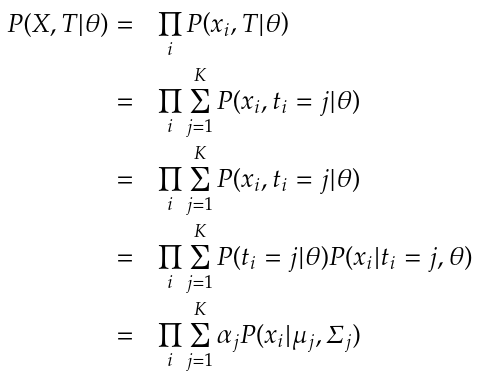EM of GMM appendix (M-Step full derivations)

This article is an extension of “Gaussian Mixture Models and Expectation-Maximization (A full explanation)”. If you didn’t read it, this article might not be very useful.

The goal here is to derive the closed-form expressions necessary for the update of the parameters during the Maximization step of the EM algorithm applied to GMMs. This material was written as a separate article in order not to overload the main one.

Ok so recall that during the M-Step, we want to maximize the following lower bound with respect to Θ :

The lower bound is defined to be a concave function easy to optimize. So we are going perform a direct optimization procedure, that is, finding the parameters for which the partial derivatives are null. Also as we already said in the main article, we have to fulfill two constraints. The first one is that the sum of mixture weights must sum up to one and the second that the covariance matrix must be positive semidefinite.

Now recall that we initially defined the probability model using a mixture of Gaussian densities like so:

This initial definition was given prior to the introduction of the latent variable t that allows us to define the probability of a specific observation belonging to a specific Gaussian. With the latent variable introduced, we now write: